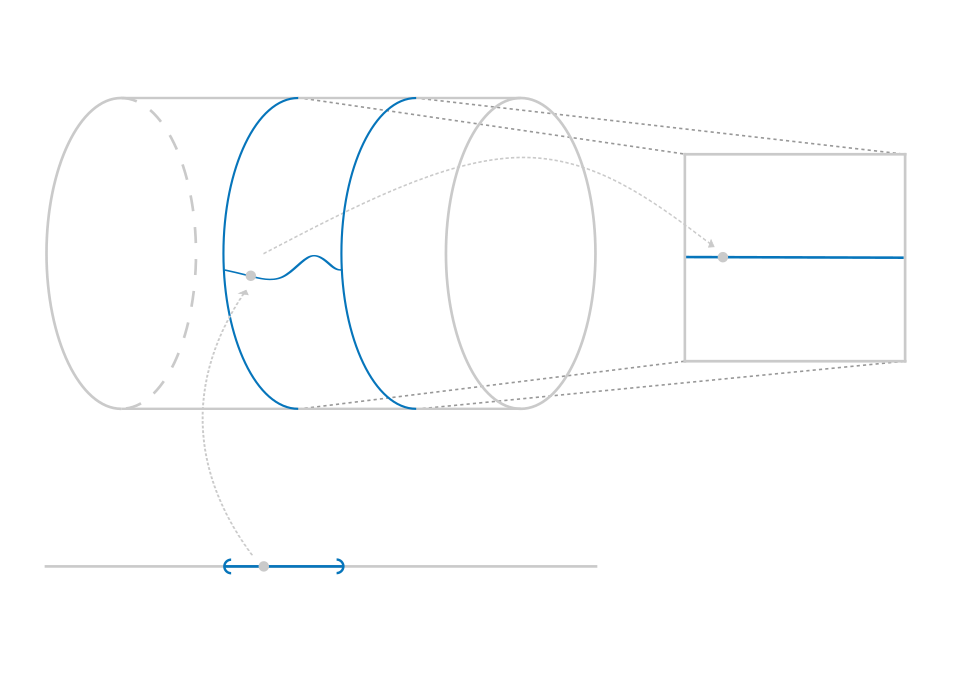
Yang-Mills Theory
My work is on Yang-Mills theory in the context of symplectic geometry. I leverage recent work on the Hodge theory of primitive forms on symplectic manifolds to study Yang-Mills connections. I am also interested in variants of the Yang-Mills functional and the regularity of their critical points.